Procvičování
Na záložkách níže najdete úkoly k procvičování látky z jednotlivých lekcí. Ke každému zadání je pro kontrolu k dispozici řešení. Silně doporučuji: Pokuste se problém nejprve vždy vyřešit sami. Mnohem víc si odnesete, než když si jen líně přečtete řešení ;-)
- Úvod a motivace
- Kategorická data a procenta
- Numerické proměnné a míry centrality
- Numerické proměnné a míry variability
- Popis vztahů mezi proměnnými
- Statistický model
- Základy inferenčního uvažování: vzorek a populace
- Pravděpodobnost, nejistota a variabilita
- Centrální limitní věta
- Centrální limitní věta 2
- Podmíněná pravděpodobnost a Bayesova věta
1
Otázka 1
Najděte, jaký je rozdíl mezi porodností (resp. hrubou mírou porodnosti) a plodností (resp. úhrnnou plodností)? V čem se liší z hlediska vhodnosti použití?
Podívat se na řešení
Porodnost, resp. hrubá míra porodnosti udává v promilích počet živě narozených na 1000 osob za kalendářní rok. Plodnost, resp. úhrnná plodnost údává průměrný počet dětí, který by se v období od 15 od 49 let věku narodil jedné ženě v dané zemi (populaci), pokud by zůstala zachována aktuální obecná míra plodnosti (tj. aktuální míra toho, jak mají ženy v různém věku děti). To může znít složitě. Důležité je rozklíčovat, že porodnost především popisuje určité časové období (přičemž nezohledňuje věkovou strukturu obyvatel), zatímco plodnost především popisuje reprodukční chování určité kohorty. Aktuální porodnost tedy může být důležitější při plánování kapacit služeb péče o děti, aktuální plodnost je zase lepším sociologickým indikátorem toho, jak moc lidé prioritizují rodičovství. Nízká plodnost může odrážet odkládání rodičovství, potíže s početím, ale také rozhodnutí větší části populace nemít vůbec děti nebo obtíže skloubit rodinu a ekonomické zajištění za podmínek stávající ekonomiky a sociálních politik.
Otázka 2
Za zjednodušeného předpokladu, že je v ČR 10 miliónů obyvatel a ročně se narodí 100 tisíc dětí, jaká je u nás hrubá míra porodnosti?
Podívat se na řešení
## [1] 10
Otázka 3
Dohledejte, jaká je aktuálně v Česku úhrnná plodnost. Dále zjistěte, jestli se zaposledních 20 let (zhruba mezi roky 2000 a 2020) zvýšila, snížila, nebo zůstala víceméně stejná.
Podívat se na řešení
Za posledních 20 let se naše úhrnná plodnost zvyšuje. Zatímco kolem roku 2000 patřila k nejnižším na světě, dnešní hodnoty kolem 1,7 z nás dělají v rámci rozvinutých zemích spíše nadprůměrnou zemi. Samozřejmě na obnovu populace to samo o sobě nestačí, na to jsou potřeby hodnoty kolem 2,1. Před úbytkem populace nás (zatím) chrání prodlužující se délka života a narůstající migrace.
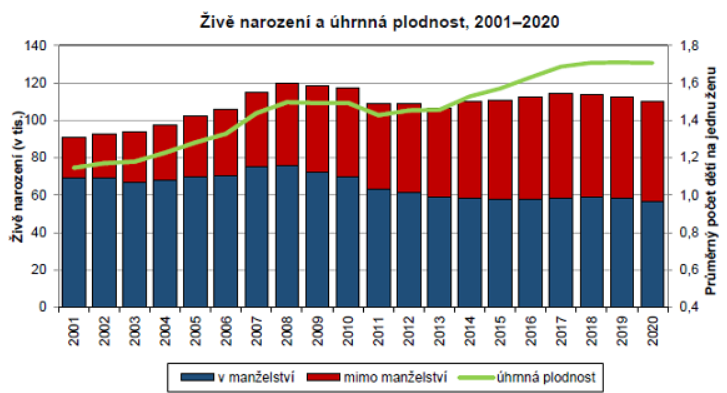
Otázka 4
Čína dnes vykazuje velmi nízkou míru plodnosti (daleko za Českou republikou). Navíc víme, že politika jednoho dítěte, která byla v minulosti realizována v Číně, vedla k tomu, že je dnes v kohortě mladých lidí v reprodukčním věku nebývalá převaha mužů. (Je to důsledkem toho, že rodiny nucené mít jen jedno dítě preferovaly chlapce do té míry, že to vedlo k selektivním potratům na základě pohlaví.) Jak bychom tuto doplňkou informaci vyhodnotili vzhledem k nízké míře plodnosti v zemi? Souhlasíte tvrzením, že nízká míra plodnosti v Číně může být do určité míry pouze zdánlivá a vyplývat z výše popsaných důsledků politiky jednoho dítěte? Proč ano/ne?
Podívat se na řešení
Je to přesně naopak. Skutečnost, že je v současné kohortě mladých tak málo žen, vlastně znamená, že nízká míra plodnosti ani plně neodráží závažnost demografické situace v Číne.
2
Otázka 1
Pro každou z následujících proměnných rozhodněte, zda jde o proměnnou nominální, ordinální, nebo kardinální. Pokud jde o proměnnou kardinální, rozhodněte také, jestli je intervalová, nebo poměrová a do třetice, jestli je spojitá, nebo diskrétní.
- Čísla na dresech hokejistů
- Velikost bydliště vyjádřená počtem obyvatel
- Náboženské vyznání: protestant - katolík – buddhista – muslim – ateista - hinduista
- Místo bydliště (obec)
- Věk měřený počtem let
- Spokojenost s pracovními podmínkami: velmi spokojen – spíše spokojen – spíše nespokojen – velmi nespokojen
- Rok letopočtu
Podívat se na řešení
- nominální, jde pouze o pojmenování, čísla na dresech neznamenají žádné pořadí v ničem
- kardinální ´- poměrová (má přirozenou 0, resp. můžeme říct, že jedna obec je třikát má třikrát více obyvatel než druhá) - diskrétní (neexistuje nic jako polovina obyvatele)
- nominální
- nominální
- kardinální - poměrová - a teď záleží, jak rozumíte měřený počtem let: pokud jste si to vyložili jako počtem celých let, pak je diskrétní, pokud tak, že roky jsou pouze jednotka, ale lze říct, že je někomu třeba 34,66 let, pak je to proměnná spojitá.
- ordinální
- kardinální - intervalová (rok 1500 je stejně daleko od roku 1000 jako od roku 2000, ale nelze říct, že pokud se něco událo v roce 2000, událo se to dvakrát později než to, co se událo v roce 1000) - diskrétní
Otázka 2
Sebevražda je od dob Émila Durkheima považována za relevantní sociologické téma. Jedno pohlaví páchá sebevraždu výrazně (asi čtyřikrát až pětkrát) častěji než druhé (označujme ho po zbytek úlohy pohlaví A). Tipněte si (bez googlování), které to je. Jaké sociologické důvody by s tím mohly být spojeny? Poté odpovězte následující otázky (čísla přibližně platí pro ČR posledních let):
- Pokud platí, že pohlaví A páchá sebevraždu čtyřikrát častěji než pohlaví B, doplňte následující větu (každé XXX nahraďte číslem, předpokládejte pro jednoduchost, že obě pohlaví jsou ve společnosti zastoupena stejně):
“Relativní riziko sebevraždy je u pohlaví A o XXa % větší než u pohlaví B. Pokud víme, že v každém roce spáchá sebevraždu asi 24 jedinců pohlaví A na 100 000 obyvatel, můžeme dopočítat, že ročně spáchá sebevraždu asi XXb jedinců pohlaví B na 100 000 obyvatel. Rozdíl v absolutním riziku spáchání sebevraždy je tedy mezi oběma pohlavímí XXc %. Šanci na spáchání sebevraždy u jedince pohlaví A, pokud nemáme žádné další informace, lze vyjádřit zlomkem XXd. [Nadstavba, nemusíte umět:] Poměr šancí spáchání sebevraždy mezi pohlavím A a pohlavím B pak lze vyjádřit číslem XXe.”
Podívat se na řešení
Pohlaví A jsou muži. To, že muži páchají sebevraždu výrazně více než ženy, je skutečností napříč společnostmi. Protože se tématem nezabývám, důvody neznám, takže váš brainstorming klidně mohl vygenerovat lepší nápady než můj. Já vycházím z toho, že za komunismu u nás muži páchali sebevraždu jen asi 2krát až 3krát častěji než ženy, zatímco dnes je to 4krát až 5krát častěji (počty sebevražd mezi ženymi poklesly od 70. a 80. let na méně než polovinu, zatímco počty sebevražd mezi muži klesly jen o přibližně 25 %). Proto si myslím, že to do nějaké míry může souviset s tím, že současné uspořádání s důrazem na soutěživost může negaitvněji dopadat na muže, kteří neuspějí, než na ženy. Další hypotéza je, že by to mohlo souviset se hustotou a kvalitou sociálních služeb - azylové domy a podobné instituce jsou často jen pro ženy, obdobné instituce pro muže jsou řidší. Ale jak říkám, je to jen brainstorming.
A teď už k číslům:
- XXa = 300 %
- XXb = 6
- XXc = 0,018 %
- XXd = 24/99976 (lze upravit na 3/12497)
- XXe = 4
V textu s vysvětlením:
“Relativní riziko sebevraždy je u pohlaví A o 300 % větší než u pohlaví B (pozor, pokud je relativní riziko 4krát větší, znamená to, že je o 300 % větší, analogicky jako 1,5krát větší riziko představuje o 50 % větší riziko). Pokud víme, že v každém roce spáchá sebevraždu asi 24 jedinců pohlaví A na 100 000 obyvatel, můžeme dopočítat, že ročně spáchá sebevraždu asi 6 jedinců pohlaví B na 100 000 obyvatel. Rozdíl v absolutním riziku spáchání sebevraždy je tedy mezi oběma pohlavímí 0,018 % (tedy necelé 2 desetiny promile - zde se opět dotýkáme toho, že velký rozdíl v relativním riziku nemusí znamenat velký rozdíl v absolutním riziku, pokud je celkové riziko malé, výpočet je následující: Absolutní riziko u mužů v procentech = (24/100000) \(\times\) 100). Absolutní riziko u žen = (6/100000) \(\times\) 100). Z obou výsledků pak už jen spočítáme rozdíl = 0,024 - 0,006. Šanci na spáchání sebevraždy u jedince pohlaví A, pokud nemáme žádné další informace, lze vyjádřit zlomkem 24/99976. [Nadstavba, nemusíte umět:] Poměr šancí spáchání sebevraždy mezi pohlavím A a pohlavím B pak lze vyjádřit číslem 4 (výpočet: (24/99976)/(6/99994)).”3
Otázka 1
Každý z následujících výroků dokončete/doplňte správnou z nabízených možností:
- Úsečka uvnitř krabice v krabicovém grafu (boxplot) znázorňuje … (a) aritmetický průměr, (b) medián, (c) modus
- Tato metrická data (2, 3, 5, 5, 7, 9, 9, 11, 12) můžeme označit za … (a) mající kladnou šikmost, (b) mající zápornou šikmost, (c) bimodální.
- Na pět stejných částí rozdělují data… (a) percentily, (b) kvartily, (c) kvintily
- Nejvíce náchylná na extrémní pozorování je tato statistika… (a) medián, (b) oříznutý průměr, (c) aritmetický průměr
Podívat se na řešení
Správné odpovědi jsou: b, c, c, c
Zdůvodnění:
- Tak je boxplot zkonstruován, je potřeba si zapamatovat.
- Data jsou dokonale symtrická, ale mají dvě nejčastější hodnoty: 5 a 9, tedy jsou bimodální
- No tak, tenhle byste uhádli, i kdybyste o tom nikdy neslyšeli…
- Prostřední hodnota se s extrémními pozorováními mění úplně stejně jako s neextrémními. Oříznutý průměr vypouští extrémní pozorování z výpočtu, čímž jejich vliv potlačuje.
Otázka 2
Za použití libovolného softwaru nebo papíru vypočítejte průměrný věk naděje na dožití kombinované populace v následujících zemích podle zadaných čísel (vážený průměr). Která země do výsledku “promluví” největší vahou?
| country | life_exp | population |
|---|---|---|
| Iceland | 82.4 | 348450 |
| Norway | 82.5 | 5295619 |
| Switzerland | 83.3 | 8484130 |
| Montenegro | 76.8 | 622359 |
| North Macedonia | 75.9 | 2075301 |
| Albania | 76.4 | 2870324 |
| Serbia | 76.3 | 7001444 |
| Turkey | 76.4 | 80810525 |
Podívat se na řešení
Protože nám nejde o průměr z ukazelů jednotlivých zemí, ale o průměr ze všech jednotlivců v těchto zemích, musíme použít vážený průměr, abychom zohlednili různou velikost populace v jednotlivých zemích. Největší vahou do výsledku promluví největší země, tedy Turecko.
data$life_exp * data$population # nejprve roznásobíme jednotlivé naděje na dožití jejich vahou, tedy populací země, které se týkají## [1] 28712280 436888568 706728029 47797171 157515346 219292754 534210177
## [8] 6173924110sum((data$life_exp * data$population)) # Tato čísla sečteme## [1] 8305068434sum((data$life_exp * data$population)) / sum(data$population) # Výsledek vydělíme součtem všech populací.## [1] 77.250594
Otázka 1
Každý z následujících výroků dokončete/doplňte správnou z nabízených možností:
- Vzorec \(\sqrt{E[X-E(X)]^2}\) je možným zápisem pro výpočet … (a) rozptylu, (b) směrodatné odchylky, (c) variačního koeficientu
- Jaký je vztah mezi rozptylem a směrodatnou odchylkou … (a) rozptyl je vždy větší, (b) rozptyl je vždy menší, (c) nelze říct
- Kterou z následujících měr variablity bychom nejspíše označili za robustní … (a) směrodatnou odchylku, (b) mezikvartilové rozpětí, (c) variační rozpětí
- Robustní statistika je taková, která … (a) není příliš ovlivněna extérmními pozorováními, (b) pro jejíž výpočet je potřeba znát hodnotu všech pozorování, (c) pro jejíž výpočet stačí znát pouze hodnotu kvartilů
Podívat se na řešení
Správné odpovědi jsou: b, c, b, a
Zdůvodnění:
- Odmocnina jednoho z běžných zápisů rozptylu, tedy směrodatná odchylka
- Rozptyl je sice smrodatná odchylka na druhou, ale pokud je směrodatná odchylka menší než 1, je rozptyl menší.
- Směrodatná odchylka vychází z rozptylu, který ve výpočtu využívá čtverec odchylky pozorování od průměru, jinými slovy dává odlehlým pozorováním velkou váhu. Variační rozpětí je zase citlivé na hodnoty maxima a minima. Jen mezikvartilové rozpětí je poměrně robustní.
- Tak je prostě robustní statistika definována, je potřeba si pamatovat
Otázka 2
Za použití tužky a papíru vypočítejte mezikvartilové rozpětí, výběrový rozptyl, výběrovou směrodatnou odchylku pro následující datovou sadu: 10, 11, 20, 13, 22, 7, 8, 19
Podívat se na řešení
Níže používám funkce v R, výsledky slouží pouze pro kontrolu, nepředpokládá se využití funkcí, spíše je dobré procvičit si výpočet v ruce.
IQR(c(10, 11, 20, 13, 22, 7, 8, 19)) # mezikvartilové rozpětí## [1] 9.75quantile(c(10, 11, 20, 13, 22, 7, 8, 19), 0.25) # 1. kvartil## 25%
## 9.5quantile(c(10, 11, 20, 13, 22, 7, 8, 19), 0.75) # 3. kvartil## 75%
## 19.25var(c(10, 11, 20, 13, 22, 7, 8, 19)) # výběrový rozptyl## [1] 33.64286n <- length(c(10, 11, 20, 13, 22, 7, 8, 19))
var(c(10, 11, 20, 13, 22, 7, 8, 19)) * (n-1)/n # populační rozptyl, ten ale skoro nikdy nechcete ## [1] 29.4375sd(c(10, 11, 20, 13, 22, 7, 8, 19)) # výběrová směrodatná odchylka## [1] 5.800246sqrt(var(c(10, 11, 20, 13, 22, 7, 8, 19))) # alernativní výpočet## [1] 5.8002465
Otázka 1
Stáhněte si dataset Countries a vypočítejte vždy Pearsonův a Spearmanův korelační koeficient pro následující dvojice proměnných. Dvojici proměnných si vizualizujte a na základě toho rozhodněte, který koeficient je vhodnější:
- Plocha a populace
- HDP a populace
- Procento univerzitně vzdělaných a populace
Podívat se na řešení
Správné odpovědi jsou:
Zdůvodnění:
- Pearson = 0.78, Spearman = 0.73. Tyto vysoké populace nejsou překvapivé, do větší zemí se vejde více lidí.
- Pearson = 0.96, Spearman = 0.85. Tyto extrémně vysoké korelace nejsou překvapivé, HDP není na hlavu, ale agregované pro celou zemi. Je jasné, že větší populace toho více vytvoří.
- Pearson = -0.17, Spearman = -0.22. Tyto záporné koralce by člověk těžko odhadoval předem - není hned jasné, proč by měl být nějaký vztah mezi procentem lidí s diplomem a velikostí populace. Každopádně vztah je to velmi slabý, jak je i patrné z grafu.
Otázka 2
Níže je popsáno několik hypotetických či skutečných příkladů Simpsonova paradoxu. Pro každý příklad zkuste vymyslet mechanismus, který by ho mohl vysvětlovat.
- Skutečný příklad: Objevila se zpráva, že ve věkové skupině osob ve věku 18-59 let je mezi očkovanými proti nemoci COVID dvojnásobná úmrtnost oproti neočkovaným. Data byla skutečná, ovšem nešlo o to, že by očkování zvyšovalo pravděpodobnost úmrtí, nýbrž šlo o příklad Simpsonova paradoxu. Dokážete vymyslet, v čem mohl spočívat?
Podívat se na řešení
V krátkosti: v dané věkové skupině nebyli lidé očkováni rovnoměrně. U starších kategorií bylo očkování mnohem častější, ale starší lidé mají také větší pravděpodobnost úmrtí.
Původní tvrzení: Vaccinated English adults under 60 are dying at twice the rate of unvaccinated people the same age. Zdroj ZDE
Professor Jeffrey Morris estimated that the annual mortality rate at the older end of the 10-59 age spectrum would be more than 50 times higher than the mortality rate at the younger end of the spectrum, with 478.2 per 100,000 deaths among 55-59 year olds and 8.8 per 100,000 among 10-14 year olds. Reuters Fact Check
Verdikt: Zavádějící. Je pravda, že ve věkové skupině 10-59 let je vyšší míru úmrtnosti u očkovaných jedinců. Není to však důsledkem toho, že by očkování způsobovalo úmrtí, ale důsledkem vyšší míry očkování u starších věkových skupin v tomto širokém věkovém rozpětí, přičemž starší mají také vyšší úmrtnost.Celý článek Reuters Fact Check
- Hypotetický příklad: Vraťte se v hlavě do USA konce 19. století, kdy míra negramotnosti v dospělém obyvatelstvu byla relativně vysoká, asi 15 % lidí nedokázalo číst. Provedete analýzu a zjistíte, že čím větší procento migrantů v daném americkém státě žije, tím nižší míra negramotnosti tam je. Znamená to tedy, že migranti jsou více gramotní než rodilí Američané? Provedete analýzu na úrovni jednotlivů a zjistíte, že je to naopak, rodilí Američané častěji dovedou číst a psát anglicky. Jde o Simpsonův paradox. Čím by mohl být způsoben?
Podívat se na řešení
Příklad jsem označil jako hypotetický, protože nejsem schopen dohledat zdroj, ale mám pocit, že jsem něco podobného skutečně četl: Například je možné, že státy s vyšší gramotností jsou ekonomicky silnější, nabízí víc pracovních příležitostí, a tak lákají více migrantů. Byť ti sami jsou méně gramotní než rodilí Američané, nepřeváží to vysokou koncentraci gramotných Američanů v bohatých státech. Na agregované úrovni pak sledujeme přesně obrácený vztah než na úrovni individuální.
6
Otázka 1
Představte si kardinální (numerickou) proměnnou, např. příjem pro tisíc lidí. Máte tedy 1000 hodnot. Nyní náhodně vyberete 1 člověka z této tisícovky, nicméně nevíte, která hodnota příjmu k němu patří. Jaký by měl být Váš nejlepší odhad jeho příjmu, pokud kritériem kvality odhadu je, že při opakování tohoto experimentu byste chtěli minimalizovat sumu čtverců odchylek skutečných hodnot od Vašich odhadů?
- Aritmetický průměr
- Medián
- Modus
- Směrodatná odchylka
- Polovina mezikvartilového rozpětí
Podívat se na řešení
Správná odpověď: aritemtický průměr
Zdůvodnění:
Z přednášky byste měli vědět, že na aritmetický průměr se můžeme dívat jako na nulový model, tedy je to taková hodnota, která minimalizuje sumu čtverců odchylek. Zároveň byste měli mít porozumění, proč odpovědi směrodatná odchylka a polovina mezikvartilového rozpětí jsou v tomto kontextu zcela nesmyslné.
Otázka 2
Které z následujících schémat je nejlepším vyjádřením toho, jak funguje statistický model?
- Pozorování = aritmetický průměr - medián
- Pozorování = predikovaná hodnota + chyba
- Pozorování = konstanta + chyba
- Pozorování = konstanta + predikovaná hodnota
Podívat se na řešení
Správná odpověď: Pozorování = predikovaná hodnota + chyba
Poznámka:
“Pozorování = konstanta + predikovaná hodnota” popisuje nulový model, tedy pokud pro odhad nepoužíváme žádné prediktory, ale pouze aritemtický průměr. Nelze tedy o obecné vyjádření toho, jak funguje statistický model.
Otázka 3
Na základě výstupu z modelu jednoduché lineární regrese určete podmíněnou očekávanou hodnotu pro jednotlivé výšky dcer. Výstup udává počátek (konstantu) a regresní koeficient nezávislé proměnné výška matky. V centimetrech.
##
## Call:
## lm(formula = childHeight ~ mother, data = Mother_Daughter)
##
## Coefficients:
## (Intercept) mother
## 110.9700 0.3182- Podmíněná očekávaná hodnota pro dceru, jejíž matka měří 150 cm
- Podmíněná očekávaná hodnota pro dceru, jejíž matka měří 165 cm
- Podmíněná očekávaná hodnota pro dceru, jejíž matka měří 190 cm
Podívat se na řešení
- Predikce (podmíněné očekávané hodnoty) výšky dcer na základě modelu jsou pro jednotlivé výšky matek (v daném pořadí): 158.71, 163.48, 171.44
Otázka 4
V rámci práce se statistickým modelem provádíme tzv. rozklad sumy čtverců reziduí (sum of squares, SS), pro který zavádíme zkratky TSS, ESS a RSS. Které z následujících vztahů platí?
- TSS = ESS - RSS
- ESS = TSS + RSS
- RSS = ESS - TSS
- TSS = RSS - ESS
Podívat se na řešení
Žádný. Všechny výše uvedené vztahy jsou špatně. Platí TSS = ESS + RSS, tedy že celková suma čtverců se rovná součtu modelem vysvětlené sumě čtverců a residuální sumy čtverců.
7
Otázka 1
Která z následujících tvrzení platí?
- S větší velikostí výběrového souboru roste validita.
- S větší velikostí výběrového souboru roste validita a reliabilita.
- S lepší reprezentativitou výběrového souboru roste validita.
- S lepší reprezentativitou výběrového souboru roste reliabilita.
Podívat se na řešení
Správná odpověď: Platí pouze tvrzení “S lepší reprezentativitou výběrového souboru roste validita.” Velikost vzorku sama o sobě ovlivňuje pouze reliabilitu.
Otázka 2
Co říká zákon velkých čísel?
- Distribuce průměrů z jednotlivých výběrových souborů se bude blížit normálnímu rozdělení s tím, jak poroste N (velikost každého jednoho výběrového souboru, ze kterých průměry počítáme).
- Pokud opakujeme náhodný výběr z populace mnohokrát, průměrná pozorovaná hodnota se bude velmi blížit skutečné hodnotě v populaci.
- Pokud pozorujeme určité subjekty opakovaně, subjekty s extrémně vysokými naměřenými hodnotami v čase T1 budou mít v čase T2 tendenci k hodnotám méně extrémním (relativně blíže k průměru ve srovnání s ostatními).
- Pokud bychom lidem přidělili percentily například jejich výšky, pak platí, že čím vyšší percentil bychom hledali, tím méně takových lidí by bylo v populaci. Například lidí na 50. percentilu by bylo méně než lidí na 90. percentilu.
Podívat se na řešení
Správná odpověď: “Pokud opakujeme náhodný výběr z populace mnohokrát, průměrná pozorovaná hodnota se bude velmi blížit skutečné hodnotě v populaci.”
Poznámka:
První možnost je popisem centrální limitní věty. Třetí možnost vyplývá z regrese k průměru. Čtvrtá možnost nereprezentuje žádnou statistickou zákonitost a je věcně špatně - lidí na 10. percentilu bude stejně jako lidí na 20. percentilu a stejně jako lidí na 50. a 90. percentilu a jako na každém jiném percentilu: 1 %. Nenechte se zmást tím, že pokud uvažujeme výšku, která bude mít přibližně normální rozdělení, tak platí, že lidé na 40. a 50. percentilu budou mít méně odlišnou výšku než lidé na 80. a 90. percentilu. To je pravda.
Otázka 3
Které parametry jednoznačně definují normální rozdělení?
- Průměr, medián a modus
- Rozptyl
- Průměr a směrodatná odchylka
- Průměr a rozptyl
Podívat se na řešení
Správné odpovědi jsou dvě: 3 a 4. Typicky sice normální rozdělení definujeme průměrem a směrodatnou odchylkou, ale rozptyl je na směrodatnou odchylku jednoznačně přímo převoditelné, takže také kombinace parametrů průměr a rozptyl normální rozdělení jednoznačně definuje.
Otázka 4
Přibližně kolik procent všech pozorování nalezneme u normálního rozdělení mezi hodnotami -nekončeno a +2sd? Zvolte nejlepší z nabízených odpovědí.
- 68 %
- 95 %
- 99,8 %
- 98 %
Podívat se na řešení
Platí varianta 98 %. Nenechte se zmást tím, že mezi -2sd a +2sd se nachází cca 95 % všech pozorování. Nyní počítáme od -nekonečna, takže bychom se dostali k 97,5 %. Ovšem to platí pro hodnoty -1,96sd a +1,96sd. Pro 2 sd je přesnější 98 %. V otevřené otázce by 97,5 % byla dostatečně přesná odpověď. V uzavřené otázce by na základě toho neměl být problém mezi nabízenými variantami vybrat jako nejlepší možnost variantu 98 %, což je o něco přesnější odpověď.
8
Otázka 1
Označme si písmeny \(y\) a \(z\) dvě události, u kterých lze jednoznačně určit, zda nastaly, nebo ne. Která z následujících tvrzení o pravděpodobnosti těchto událostí zcela jistě NEplatí?
- \(Pr(z) = 2\)
- \(1 - Pr(z) = -0.3\)
- \(Pr(y) = 0.2\) & \(Pr(y)+ Pr(z) = 0.1\)
- \(Pr(y)+ Pr(z) = 1\)
Podívat se na řešení
Zcela jistě neplatí první tři možnosti. Pravděpodobnost z definice nemůže být větší než 1, což zneplaťnuje první dva výroky. Pravděpodobnost také nemůže být záporná, což zneplatňuje třetí výrok.
Otázka 2
Hustota pravděpodobnosti (PDF) výsledku určitého experimentu, který může nabývat čtyř různých stavů (vzájemně se vylučujících), je vyjádřena obrázkem níže. Určete na základě PDF a základních pravidel počítání s pravděpodobností následující:
- \(Pr(A)\cup Pr(C)\) v jednom opakování experimentu
- Pravděpodobnost, že v pěti po sobě jdoucích nezávislých experimentech dostaneme vždy výsledek B
- Pravděpodobnost, že ve dvou nezávislých opakováních experimentu získáme v prvním experimentu výsledek B nebo D a ve druhém A nebo C?

Podívat se na řešení
- 0.1 + 0.3 = 0.4
- 0.4^5 = cca 0.01, tedy asi 1 %
- 0.6 * 0.4 = 0.24
Otázka 3
Zodpovězte následující:
- Pokud víme, že výsledek experimentu může nabývat 20 různých stavů, jejichž rozdělení je uniformní, jaká je pravděpodobnost, že nastane 16. z těchto 20 stavů?
- Jaká je očekávaná hodnota hodu spravedlivou šestistěnnou kostkou?
- Jaké parametry zcela definují Alternativní rozdělení?
Podívat se na řešení
- 1/n, tedy 1/20 = 0.05 neboli 5 %. Že se jedná o 16. stav je redundantní informace, všechny stavy mají v uniformním rozdělení stejnou pravděpodobnost.
- 3.5 … tuto hodnotu lze vypočítat jako aritmerický průměr z hodnot 1 až 6 nebo vzorcem pro uniformní rozdělení “(minimum + maximum)/2”.
- Jde o jediný parametr, pravděpodobnost úspěchu, který značíme zpravidla \(p\).
9
Otázka 1
Která z tvrzení o CLT platí?
- Díky CLT víme, že každá proměnná bude mít při dostatečném počtu pozorování přibližně normální rozdělení.
- CLT říká, že (téměř) nehledě na distribuci původní proměnné můžeme určit, kde se vyskytuje prostředních 95 % procent všech pozorování: přibližně mezi -2 a +2 směrodatnými odchylkami.
- CLT říká, že (téměř) nehledě na distribuci původní proměnné bude mít průměr z výběorových souborů (vzorků) tendenci k normálnímu rozdělení s dostatečně velkým n (velikostí jednotlivých vzorků).
- Díky CLT dokážeme konstruovat inervalové odhady průměru proměnné, téměř nehledě na distribuci proměnné, pro kterou průměr určujeme, pokud máme dostatečně velký výběrový soubor.
Podívat se na řešení
Platí druhé dva výroky. První dva představují možné chybné interpretace. Ujistěte se, že rozumíte, proč jsou špatně. CLT nám neříká nic o distribuci proměnné. Její výpověď se vztahuje k distribuci agregující/sumarizační statistiky (typicky průměru nebo sumy) v hypotetickém případě, že bychom výběr z populace opakovali mnohohrát.
Otázka 2
Jaký výraz na obrázku představuje standardní chybu?:
- \(\sigma\)
- \(\frac{\sigma}{\sqrt n}\)
- \(\mu\)
- \(\bar x\)
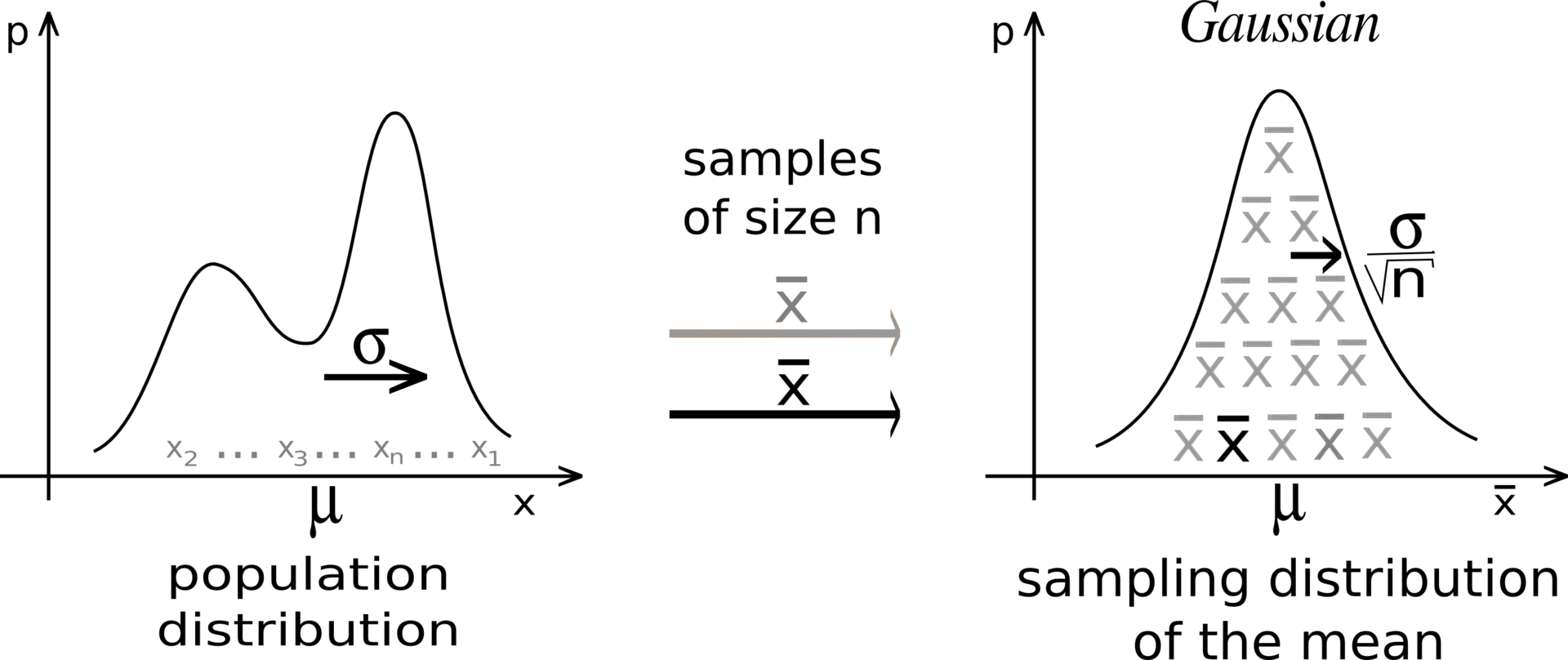
Podívat se na řešení
Správná odpověď:
\(\frac{\sigma}{\sqrt n}\)
Otázka 3
Převeďte následující hodnoty na z-skóry: 90, 95, 98, 100, 100, 102, 145
Poznámka: pro výpočet rozptylu použijte vzorec pro výběrový rozptyl, tedy:
\[ rozptyl = \frac{\sum (x_i - \bar{x})^2}{n-1} \]
Podívat se na řešení
## [1] -0.777 -0.505 -0.342 -0.233 -0.233 -0.124 2.214Z-skór je převedení hodnot na takové hodnoty, které mají průměr 0 a směrodatnou odchylku 1. Výpočet jsme si ukazovali: od hodnot odečteme jejich průměr a vydělíme směrodatnou odchylkou. V Excelu je potřeba použít funkci “SMODCH.VÝBĚR.S” pro výběrovou směrodatnou odchylku.
Otázka 4
Jaká je pravděpodobnost, že dané pozorování bude mít z-skór menší nebo roven hodnotě -1?
Podívat se na řešení
To nelze jednoznačně určit. Tahle otázka byla trochu chyták, ale ne samoúčelný. Abyste mohli na otázku odpovědět, museli byste vědět, z jakého rozdělení pozorování pochází. Z-skóry typicky používáme v kontextu normálního rozdělení, nicméně spočítat je můžeme pro jakékliv rozdělení (pokud známe průměr a směrodatnou ochylku). (Pro zájemce: existuje tzv. Chebyshevův teorém, který určuje alespoň hranice podílu pozorování, která jsou oddělena určitým počtem směrodatných ochylek, i pro distribuce, které nejsou normální. Z hlediska kurzu je to ale nadstavba k případnému samostudiu.)
Otázka 5
Pokud víme, že náhodné pozorování pochází z normálního rozdělení, (A) jaká je pravděpodobnost, že bude mít z-skór menší než -1? (B) A jaké je pravděpodobnost, že bude mít z-skór větší než +1,5? (C) A větší nebo roven 1,5?
Podívat se na řešení
15,9 %, v Excelu: “=NORM.S.DIST(-1;PRAVDA)”
6,7 %, v Excelu: “=1-NORM.S.DIST(1,5;PRAVDA)”, případně “=NORM.S.DIST(-1,5;PRAVDA)” … na těchto dvou variantách si hezky můžete uvědomit jak se chová symetrie normálního rozdělení.
Stejné jako (B). Pohybujeme se ve spojitém rozdělení, takže na tom nezáleží: pravděpodobnost každé přesné hodnoty je 0, takže dodatek “nebo rovno” nic nemění. Amazing, co?
Otázka 6
Která z následujících interpretací konfidenčního intervalu (ve frekventistickém paradigmatu) je správná?
95% konfidenční interval znamená, že…
- … 95 % pozorování původní proměnné leží v tomto intervalu.
- … u 95 % opakovaných experimentů by sledovaná statistika spadla do tohoto intervalu.
- … existuje 95% pravděpodobnost, že daný interval překrývá skutečnou populační hodnotu.
- … pokud bychom náš experiment realizovali mnohokrát, interval by v 95 % případů překrýval skutečnou populační hodnotu.
Podívat se na řešení
Jen ta poslední. Ty ostatní jsou všechny problematické:
- … 95 % pozorování původní proměnné leží v tomto intervalu. - nesmysl, interval spolehlivosti není o pozorováních, ale o hodnotě statistiky, která popisuje výběrový soubor
- … u 95 % opakovaných experimentů by sledovaná statistika spadla do tohoto intervalu. - lepší, ale ne. Interval spolehlivosti se nevtahuje k tomu, jak by dopadly další podobné experimenty, ale k populační hodnotě.
- … existuje 95% pravděpodobnost, že daný interval překrývá skutečnou populační hodnotu. - tohle je hodně otázka filosofie toho, co je to pravděpodobnost, ale ve frekventistickém paradigmatu to neplatí. Frekventisté říkají: populační hodnota je daná a interval ji objektivně buď překrývá, nebo ne. End of the story, žádná pravděpodobnost. To, že my populační hodnotu neznáme a nevíme jistě, jak to je, to je jiný příběh. Proto frekventistická statistika ve své striktní podobě uznává jen tu čtvrtou interpretaci. #SeSTimSmir
10
Otázka 1
Jaká je pravděpodobnost, že dané pozorování bude mít z-skór menší nebo roven hodnotě -1?
Podívat se na řešení
To nelze určit. Tahle otázka byla trochu chyták, ale ne samoúčelný. Abyste mohli na otázku odpovědět, museli byste vědět, z jakého rozdělení pozorování pochází. V kurzu Statistika 1 se zabýváme jen z-skóry v normálním rozdělení. Jako sociolog jsem se za svoji kariéru asi nesetkal s využíváním z-skórů v jiném kontextu než právě v normálním rozdělení.
Otázka 2
(A) Pokud víme, že pozorování pochází z normálního rozdělení, jaká je pravděpodobnost, že bude mít z-skór menší nebo roven hodnotě -1? (B) A jaké je pravděpodobnost, že pozorování z této distribuce bude mít z-skór větší než +1,5? (C) A větší nebo roven 1,5?
Podívat se na řešení
15,9 %, v Excelu: “=NORM.S.DIST(-1;PRAVDA)”
6,7 %, v Excelu: “=1-NORM.S.DIST(1,5;PRAVDA)”, případně “=NORM.S.DIST(-1,5;PRAVDA)” … na těchto dvou variantách si hezky můžete uvědomit jako se chová symetrie normálního rozdělení.
Stejné jako (B). Pohybujeme se ve spojitém rozdělení, takže na tom nezáleží: pravděpodobnost každé přesné hodnoty je 0, takže dodatek “nebo rovno” nic nemění. Amazing, co?
Otázka 3
Ve všech následujících případech platí, že údaje pochází z dostatečně velkého výběrového souboru, takže se můžete spolehnout na centrální limitní teorém. Spočítejte 87% interval spolehlivosti pro odhad průměru, pokud víte, že:
- průměr je 300, standardní chyba je 20 a počet pozorování je 100
- průměr je 60, směrodatná odchylka je 30 a počet pozorování je 1000
- průměr je 15 800, rozptyl je 1 000 000 a počet pozorování je 250
Podívat se na řešení
- <269,7 ; 330,3>
- <58,6 ; 61,4>
- <15704 ; 15896>
Nejprve musíte najít z-skór. Je potřeba si uvědomit, že inteval spolehlivosti má překrýt 87 % prostřeních hodnot, nicméně z-skór v tabulkách nebo softwaru vyhledávat pro pravděpodobnost od -nekonečna až do určitého bodu. Takže potřebujete najít z-skór pro pravděpodobnost 93,5 % (v Excelu pomocí funkce norm.s.inv). Pak už je to jednoduché. Je potřeba si jen dopočítat standardní chybu. V prvním případě ji už máte, takže počet pozorování nevyužijete. Ve druhém a třetím případě musíte z rozptylu, resp. směrodatné odchylky dopočítat pomocí počtu pozorování směrodatnou chybu.
11
Nečekám, že to bude hrát rozdíl ve vašem zájmu si provičovací úkoly projít, nicméně podmíněná pravděpodobnost nebude součástí závěrečné zkoušky.
Otázka 1
Máte v plánu piknik, ale probudíte se do zamračeného rána. Jaká je pravděpodobnost, že bude pršet, když také víte…
- 50 % všech deštivých dnů začíná zamračeným ránem
- Zamračená rána jsou častá, v této roční době jich je 40 %
- Dlouhodobý trend ukazuje, že v tomto měsíci jsou deštivé průměrně 3 ze 30 dní
Podívat se na řešení
Co víme:
- Pr(déšť) = 0,1
- Pr(zamračeno) = 0,4
- Pr(zamračeno|déšť) = 0,5
Takže Pr(déšť|zamračeno) = … dosadit do Bayesovy věty…
\[ \frac{0.1*0.5}{0.4} = 0.125 \]
Pravděpodobnost deště je 12,5 %. Ještě bych se s piknikem neloučil.